Have you ever contemplated about converting your knowledge over data structures and algorithms into real world applications? Or has any real world application ever fascinated you to spend some time on thinking what data structure or algorithm would that be based on? If yes, then we are on the same page. I have already tried to explore real world applications like blockchain, social-networking, computer-networks, cryptography and many more through core algorithm concepts, and undoubtedly it is a great fun doing the same as well.
One amongst all the applications, is the friend network graph used by various social networking platforms that has fascinated me the most in terms of its extensive applications of graphs. This article is more of a demonstration through which I explored and understood graph algorithms, and would strongly suggest the same to the related beginners out there as well.
So how to derive this vast network on a paper?
As an instance, two people on a social networking platform can be represented by nodes and an edge between them can determine the friendship between them.
An undirected edge can demonstrate that both are friends of each other or both follow each other, while a directed edge would mean that only one among them follow the other person in the direction of the edge.
Simple isn’t it?..
Now, How do we traverse the graph to get insights?
There are two basic algorithms than can be thought of for graph traversals -*Breadth First Search and Depth First Search.
Breadth First Search, being a level order traversal, would be quite efficient over Depth First Search for many business based insights, like the following:
- Finding all the friends of all the people in the network
- Finding all the mutual friends for a node in the network
- Finding the shortest path between two people in the network
- Finding the nth level friends for a person in the network
We can find the path between two people by running a BFS algorithm, starting the traversal from one person in level order until we reach the other person or in a much optimised way we can run a bi-directional BFS from both the nodes until our search meet at some point and hence we conclude the path , whereas DFS being a depth wise traversal may run through many unnecessary sub-trees, unknowing of the fact that the friend could be on the first level itself.
Moreover, in order to find friends at nth level, using BFS this could be done in much less time, as this traversal keeps account of all the nodes in each level.
Below is a code based demonstration of how can we determine nth-Level friends for a random person in the friend network
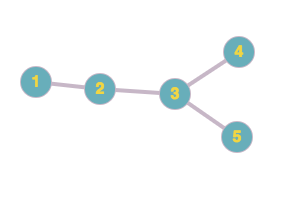
Bob uses a social networking site which has a provision that two users with ids 1 and 2 can become friends when 1 sends a friend request to 2 and 2 accepts the same friend request and vice versa. So if 1 and 2 are friends of each other and 2 and 3 are friends of each other, then with respect to source user 1, 2 is a first level friend and 3 is a second level friend, and vice versa. Similarly if 4 and 5 are friends of 3 then with respect to 1, 4 and 5 are third level friends of 1, and vice versa.
Bob represents the n users on the social media network by their user ids as 1,2,3….n.
Let’s consider…
Input Format The first line of the input denotes the total number of users (n) in the social media network. This is followed in the next line, by friend pairs represented as space separated user-ids p q (where p and q are ids of two users who are friends of each other). All friend pairs are terminated by a new line. The input of these pairs will be terminated by a pair -1 -1 (to denote the end of input of friend pairs) The last line of input takes source user-id s and level k separated by a space.
*Output Format *The output consists of space separated friend-ids which are present at level k from the source friend-id s. If no friend present at level k then print 0
Sample Input
0 6
1 2
1 3
2 4
3 6
4 5
-1 -1
1 2
Sample Output
4 6
*Explanation *In the given input, there are 6 people in the network, i.e. we have 6 user ids. For the given friend pairs 1 2 and 1 3, it is obvious that 2 and 3 are level 1 friends of user 1 and vice versa whereas 4 is level 1 friend of user 2 and 6 is level 1 friend of user 3. So it is clear that 4 and 6 are level 2 friends of user 1. Hence for source 1 and level 2 output is 4 6.
Let’s dive into the solution now….
Consider the below figure of a friend network graph with 5 users in the network:
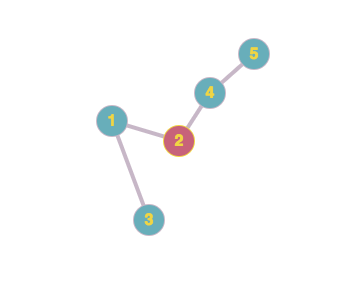
Let’s write all level friends for each user in {1,2,3,4,5}:
For user 5
- Level 1–4
- Level 2–2
- Level 3–1
- Level 4–3
For user 4
- Level 1–2,5
- Level 2–1
- Level 3–3
For user 3
- Level 1–1
- Level 2–2
- Level 3–4
- Level 4–5
For user 2
- Level 1–1,4
- Level 2–3,5
For user 1
- Level 1–2,3
- Level 2–4
- Level 3–5
As you can observe, friends at level k , vary for each source node/user.
How about the algorithm now?…
You can implement BFS by two data-structures:
**Adjacency Matrix **— O(n²) time complexity where n is the number of nodes(users) in the graph
**Adjacency List** — O(V+E) time complexity where V is the total no. of nodes and E is the total no of edges in the graphAdjacency Matrix Implementation
n — input : total no. of users in the network
adj[n][n]- to represent the adjacency matrix filled with all zeros except for edges set to 1. If there is an edge from 1 to 2 (1 and 2 are direct friends), set adj[1][2]=1 and adj[2][1]=1
visited[n]- an array to mark the nodes which are visited, initially visited[n]={0} for all nodes source — input: source node/user.
levels[n]- represents the level number. Eg: level[i]=k i.e. node i is present at level k from source. level[source]=0
level- input : level k, to find the friends at that level.
The above solution coded in any programming language will work. Since the worst case time complexity of the adjacency matrix is O(n²) you can still improve this with adjacency list.
Adjacency List Implementation
Following is the C++ implementation of the program using adjacency list
The above implementation works fine when we have less number of users. What if we have thousands of millions of users in the social network?
The biggest challenge here is to storing the huge user’s data and the relationships between each of them. This is where, Neo4j also known as The Leader of Graph Databases gets the spotlight.
Why Neo4j ?
Graph databases like Neo4j proves much faster than relational databases, when it comes to graph traversals, storing relationships as friend or friend-of-friend or friend of friend of friend and so on and traversing them becomes too easy and fast in graph databases, as we store all sought of relationships alongside data in model, i.e. no expensive JOIN operations anymore.
Hurray!!
*Aleksa and Jonas built a query for finding friends-of-friends in both MySQL and Neo4j with a database of 1,000,000 users and the results were quite striking.(Refer table below)
Execution Time is in seconds, for 1,000 users.
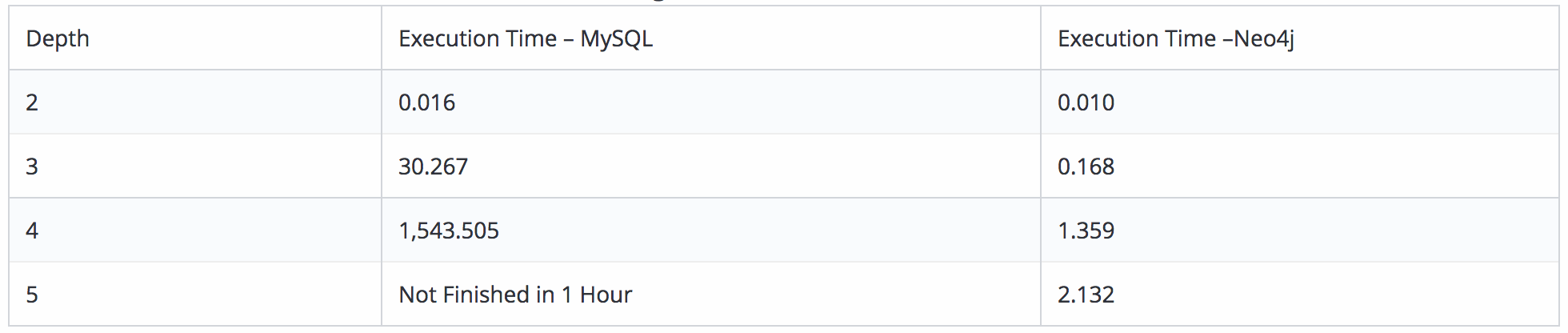
Internally, Neo4j uses a fast bidirectional breadth-first search algorithm if the predicates can be evaluated whilst searching for the path.
So, how do we tap Neo4j majestic powers to solve our problem?
Neo4j uses CQL (cypher query language) to query graph databases for storing the graph nodes (used to represent entities and its properties) and relationships(edge between nodes with properties).
Here, users are represented in form of nodes with attributes namely id and name.
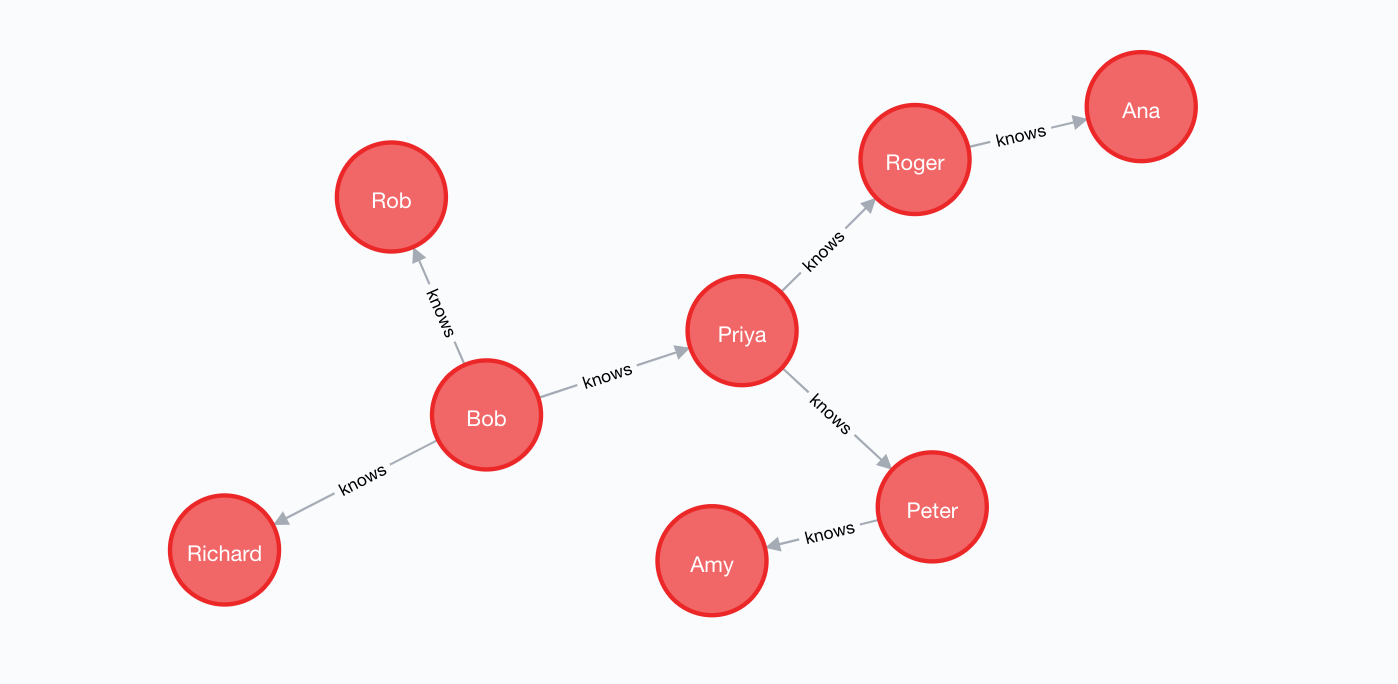
The directed relationship :knows between two nodes signifies that a node knows the other node or is friend of the other node. Like below Bob knows Priya, Richard and Rob.
Following is a combination of query statements used to create above network and store it in the graph database.
Not going into the depths of CQL syntax, I would like to explain you only the essentials here to understand the solution.
**Create** : creates a node
**( )** : represents a node
**{ }** : attributes can be assigned to a node within curly braces
**-[ ]-** : used to represent a relationship between nodes
**<- ->** : arrows can be used to represent directed edgeIn the 1st line of code User is a label given to the* first *node and Bob is a variable to access the first node.
Each node has two attributes id and name.
create (Bob)-[:knows]->(Priya)The above snippet creates a friend-relationship labeled by :knows between node Bob and node Priya.
Time to use the majestic powers of CQL with Neo4j!!
Let the source be Bob, then the query for returning all the kth level friends of Bob would be the following:
As simple as ABC.
If k=3, this will return the following as an output:

In the above query statement:
**Match** : used to match the pattern which is the basis of search/traversal
**Where** : used to compare an attribute of the node
**Return** : used to return the expected resultant data, that qualifies the Match statementAs it can be seen, how Neo4j makes the solution to our problem so handy and intuitive.
Neo4j database is truly a majestic and useful technology for product based companies, especially in the fields of business, analytics, AI, networking, etc. which deals with data in form a heap of nodes and relationships between them.
This was a precise demonstration of how one can exploit a data structure or algorithm and play with it, in order to understand it in the best ways possible and implement the same in real world projects with a few modifications into it. In addition to that, how real world technologies like Neo4j are using the same graph algorithms in order to perform the same tasks in a much simpler and faster way.
If you have suggestions or thoughts to share then please let me know!